Improving the performance of your code can be a challenging task. As software engineers, we often focus on time - how quickly did this algorithm run? However, this approach does not always yield the correct answer. Many factors contribute to optimizing performance and algorithm efficiency. Some factors are outside of our control, such as the specifications of the machine or other background programs that the machine is performing while the code runs, even the language the algorithm is written in. This is where understanding time complexity and Big O notation can come in handy.

In our industry, there are numerous concepts that we need to comprehend, and often we feel ashamed when we forget or fail to recall them. However, Big O is not one of those concepts that we should overlook. It is a fundamental concept that extends beyond computer science and can be applied in various aspects of life. After reading this blog post, I hope you will have a better understanding of Big O and appreciate its importance.

Before we dive into this post, it is crucial to emphasize the significance of Big O and time complexity in computer science and software engineering. Inefficient code is something that we strive to avoid at all costs. I must admit that I have been guilty of not being diligent enough in the past. This post serves as a reminder to not only myself but to anyone who reads it, to always keep time complexity in mind when writing any code. It is a fundamental building block for achieving optimal performance and efficiency. In this blog post, we will explore what Big O notation is and why it is crucial to understand time complexity in algorithms. And if you're already familiar with Big O, I hope you will have a better understanding of it and appreciate its importance.

What is Big O notation?

Big O is not an algorithm in itself; instead, it is a model used to measure the performance and efficiency of the algorithm that you are creating. Big O specifically describes the worst-case scenario, and provides a way to measure how the execution time of an algorithm grows as the input size increases.

Others may use the term "time complexity" when defining Big O. Time complexity refers to the amount of time it takes for an algorithm to run given it's input size (if any). Input can take various forms, such as function parameters, data sourced from databases, configuration files, and so on.

Let's say we have two functions that take a parameter, where one accepts an array of strings, and the other accepts a single string. Both running on the same machine. When the function that accepts the array of strings is called, it needs to iterate through each string in the array and output them individually.

On the other hand, the function that accepts a single string just returns the input string. The execution time of the functions will differ depending on the input size right? With larger inputs taking more time to execute. That's where Big O comes in.

It's important to note that Big O notation doesn't measure the exact speed of your algorithm in seconds or any other time unit. Remember, those factors are out of the programmers control, hence why I said "Both running on the same machine" in the example above. What we can control is the number or operations our algorithm performs.

Big O notation helps you determine the time complexity of your code by analyzing the relationship between the input size and the number of operations your code performs. By understanding the time complexity of your code, you can optimize it to run more efficiently, particularly when handling larger inputs.

In this series, we'll talk about O(1), O(log n), and O(n).

Big O notation visualized

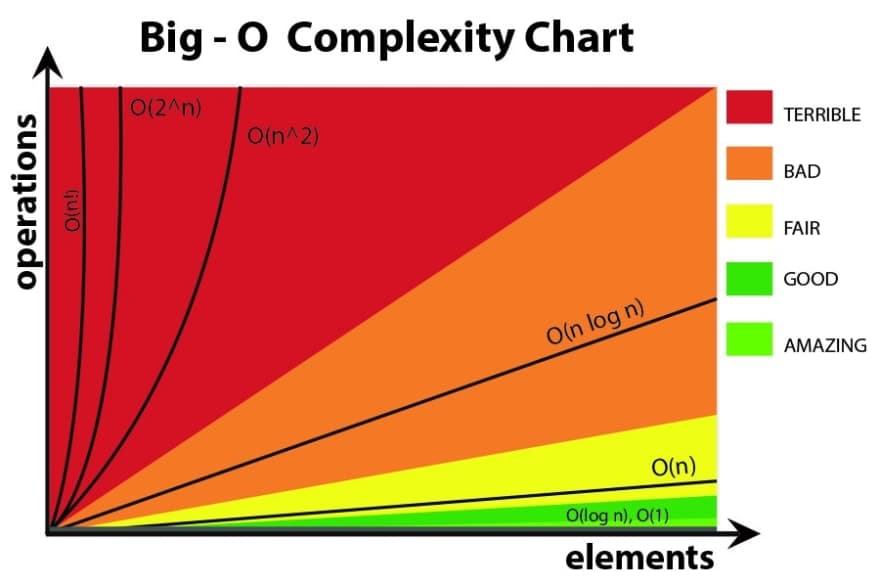
O(1) - Constant Time Complexity

What is constant time complexity? Well, forget the term time complexity for now. O(1) is an algorithm that does not depend on the input size. Regardless of the size of the input, the algorithm will always take the same amount of time to complete. So the 1 in this operation represents a constant, fixed number of operations (time complexity). Consider the example below.

An algorithm that is accessing an element in an array by its index. It takes the same amount of time, or constant time, to retrieve an element regardless of the array's length.

Regardless of the length of the array, the time it takes to retrieve an element by index remains constant. Whether the array contains 5 elements or 5000 elements, accessing an element by index takes the same amount of time because the index directly points to the desired element (in the memory).

O(log n) - Logarithmic time complexity

Logar - what? Okay this is a math term. If you're familiar with Big O, likely not the first time you're hearing it, but it's good to know what it means. To understand O(log n), we need to first understand what a logarithm is.

A logarithm is the power to which a number must be raised in order to get some other number. For example, the base ten logarithm of 100 is 2, because ten raised to the power of two is 100:

log 100 = 2 // 10^2 = 100

O(log n) represents logarithmic time complexity. It indicates that the runtime of an algorithm increases logarithmically as the input size (n) grows. In simpler terms, as the input size increases, the time taken by the algorithm grows, but not proportionally. Instead, it grows in a logarithmic manner.

An algorithm that utilizes a binary search represents O(log n) time complexity. We'll discuss what a binary search algorithm is in another series. Think of it like dividing the problem or data into smaller and smaller portions with each step.

With each iteration, the algorithm reduces the search range by half, making it more efficient for large arrays. This behavior results in a logarithmic time complexity of O(log n). As the input size increases, the algorithm needs to perform more operations, but not linearly. Instead, it grows in a slower, logarithmic manner.

O(n) - Linear time complexity

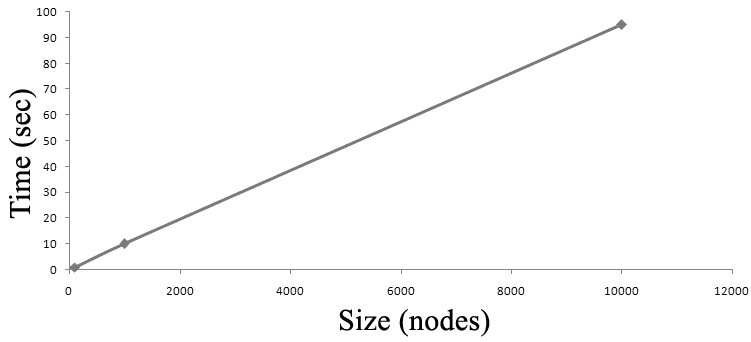
Now this is where it's starts to get a little tricky. O(n) represents linear time complexity. n is a constant value. It indicates that the runtime of an algorithm increases linearly with the input size (n). As the input grows, the time taken by the algorithm to complete also grows.

This linear increase can be represented as a straight line on a graph.

Now let's see it in code.

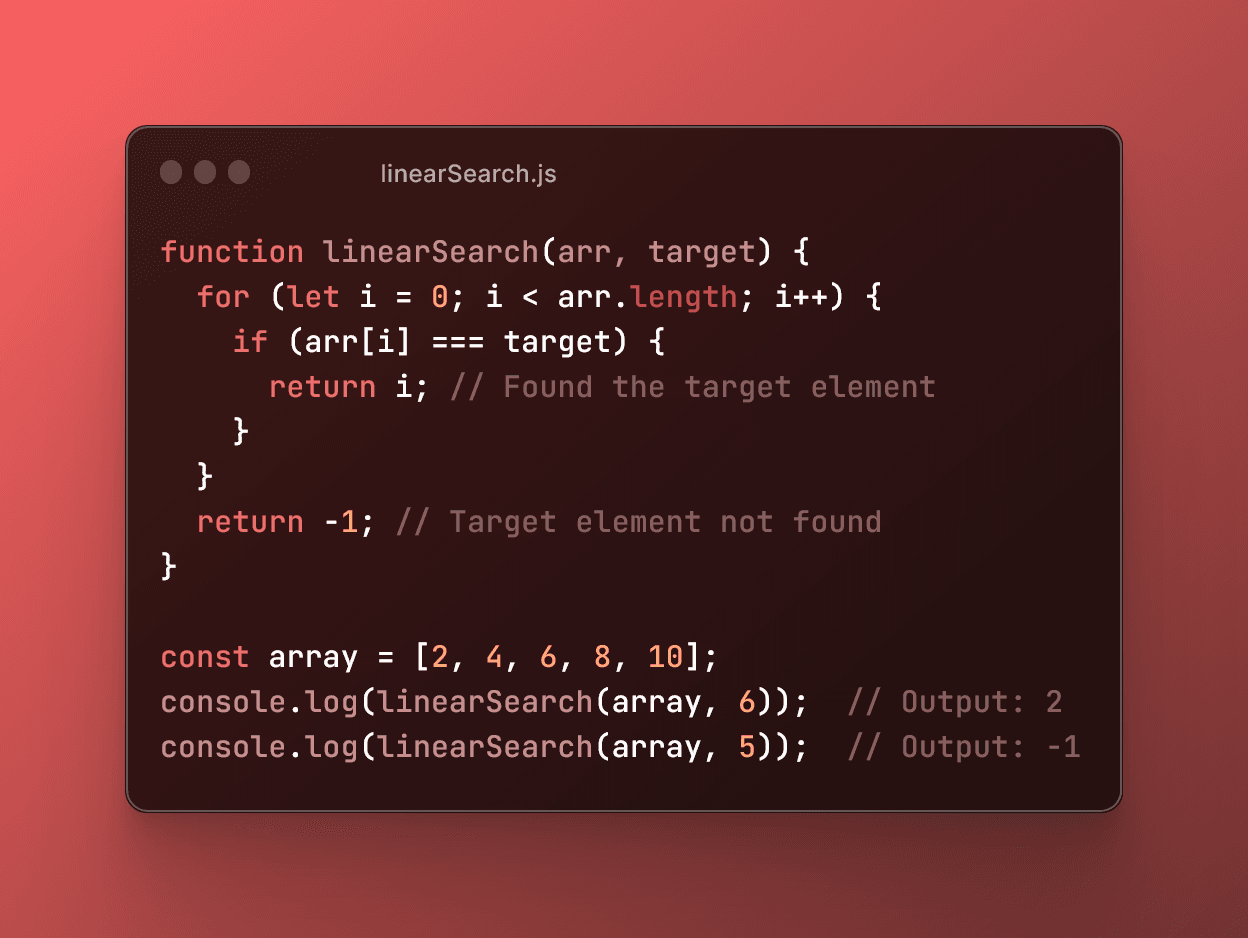
The time complexity of this algorithm is O(n) because the number of iterations in the loop is directly proportional to the size of the input array. As the array size (n) increases, the algorithm will take a longer time to complete since it needs to examine each element in the array.

Closing Remarks

Understanding the time complexity of algorithms is a fundamental skill for software engineers. In this post, we explored three important time complexities: O(1), O(log n), and O(n). O(1) represents constant time complexity, where the execution time remains constant regardless of the input size. O(log n) signifies logarithmic time complexity, where the execution time grows slowly as the input size increases. Finally, O(n) represents linear time complexity, where the execution time increases proportionally with the input size.

By being aware of these time complexities, you can make informed decisions when designing and analyzing algorithms. Consider the nature of the problem, the available data structures, and the desired efficiency to choose the appropriate algorithm. Remember, the goal is to optimize performance and reduce unnecessary overhead.

As you continue your journey as a software engineer, keep honing your understanding of time complexity and Big O notation. Practice analyzing and optimizing algorithms to improve efficiency in your projects. By mastering these concepts, you'll be equipped to write better code, solve complex problems, and contribute to the advancement of software engineering.

Until next time, Happy Computing!!

RO out 🎤